Como uma inteligência artificial funciona - redes neurais

A Inteligência Artificial é uma das tecnologias que mais cresce atualmente e está presente em diversas aplicações do nosso dia a dia, como assistentes virtuais, carros autônomos e sistemas de recomendação. Uma das áreas mais importantes da Inteligência Artificial é o Machine Learning, que permite que os sistemas aprendam a partir dos dados sem serem explicitamente programados.

Neste artigo falaremos a respeito de uma das técnicas mais poderosas e versáteis do Machine Learning que são as redes neurais, aprendendo inclusive a implementar uma do zero em Python.

O que são redes neurais?

As redes neurais são algoritmos modelados com base no funcionamento dos neurônios biológicos. Cada um dos neurônios, também chamados de perceptron, podem estar interconectados uns com os outros em diferentes camadas.

Basicamente, o perceptron é uma simples unidade de processamento de informações, ele possui duas funções: a de soma, que vai juntar os valores de todas as entradas multiplicadas por seus respectivos pesos e a de ativação, que vai pegar o valor da função de soma e transformar em uma saída, que vai variar de acordo com a ativação escolhida. Por exemplo, a função step, retorna 0 se o valor estiver abaixo de um determinado limiar e 1 se estiver acima.

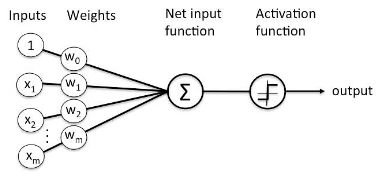
Quando conectados em sequência, em diferentes camadas, os perceptrons possibilitam a criação de funções mais complexas que podem se ajustar melhor aos dados e produzir padrões interessantes. O que vai determinar a eficiência da rede são os pesos, que podem ser entendidos como a relevância que cada parâmetro de entrada tem para obter o padrão de comportamento esperado, ou seja, os pesos são o “conhecimento” da rede.

Como as redes aprendem - algoritmos de otimização

A parte mais interessante é como fazemos para achar o valor de cada peso, a abordagem mais simples seria testar por força bruta cada possível combinação de pesos. O que para problemas muito simples pode até funcionar, mas conforme a complexidade do problema aumenta, se torna inviável testar cada possibilidade de combinação. Essa prática se torna ineficiente pois a cada novo teste que é feito, a rede está começando do zero.

Nesse ponto é que entram os algoritmos de otimização, que fazem com que a rede se adapte de acordo com os dados de teste, por exemplo, digamos que nós geramos uma rede com pesos aleatórios e o resultado retornado foi 0.8, enquanto o resultado esperado era de 1, então nós geramos outra rede e testamos novamente, dessa vez o resultado obtido foi 0.9, o que ainda não é o resultado que queremos, mas já está mais próximo do que o 0.8.

Existem diversos tipos de algoritmos que farão essa busca pelo melhor valor dos pesos, mas o importante é saber que ainda não existe um consenso sobre qual é o melhor, afinal esta ainda é uma área de estudo pelos cientistas e a combinação de diferentes técnicas pode resultar em um algoritmo que é mais rápido e gasta menos recursos, então é necessário ver os trabalhos que já foram feitos, o que está sendo feito agora e tentar adaptar para cada problema.

Um desses algoritmos é chamado de gradiente descendente, que é utilizado para otimizar funções matemáticas, em resumo, o objetivo é encontrar o mínimo (ou o máximo) de uma função. O algoritmo funciona iterativamente, ou seja, em cada iteração que ele faz uma pequena atualização nos parâmetros da função que está sendo otimizada. Essa atualização é feita na direção do gradiente, que é uma medida da inclinação ou declive da curva de função em um determinado ponto. Nesse algoritmo é utilizado a derivativa para saber se o valor está aumentando ou diminuindo em relação ao anterior e poder atualizar os pesos junto de outro algoritmo chamado de backpropagation.

Outra possível abordagem, além da pura matemática, é utilizando os algoritmos genéticos, que buscam simular o processo evolutivo dos seres vivos. Primeiro é criada uma população de diferentes redes neurais com pesos para cada conexão definidos de forma aleatória, então os indivíduos são testados e a cada um deles é atribuído um score, também chamado de fitness, que será utilizado para determinar a probabilidade de um indivíduo ser selecionado para fazer o crossover e criar os próximos indivíduos da população. Quanto maior o fitness, maior a probabilidade.

Programando uma rede neural do zero

A seguir criaremos uma rede neural para exemplificar, utilizando um problema simples de classificação binária. Primeiro vamos definir o problema, teremos um conjunto de dados com duas variáveis de entrada (x1 e x2) e uma variável de saída (y), que pode ser 0 ou 1. Nosso objetivo é treinar uma rede que seja capaz de classificar as entradas corretamente.

Para simplificar o problema, vamos gerar um conjunto de dados com 500 exemplos, cada exemplo terá duas variáveis de entrada geradas aleatoriamente a partir de uma distribuição uniforme entre 0 e 1, se a soma das duas variáveis for maior que 1, a variável de saída será definida como 1, caso contrário, deverá retornar 0.

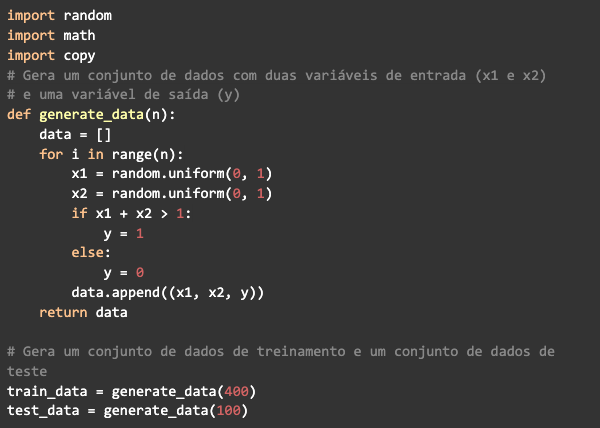
Criaremos também uma função de ativação para os neurônios, neste exemplo utilizaremos a sigmóide:

Em seguida, criaremos a classe da rede neural e iniciaremos os pesos de forma aleatória. Essa rede vai ter uma topologia fixa, com dois neurônios de entrada conectados a três neurônios ocultos e esses três neurônios ocultos estarão conectados ao neurônio de saída.

Na inicialização da rede também é opcional passar uma lista de pesos, isso vai ser importante para gerar a nova população depois do crossover. Há uma condição para definir os pesos, se a lista estiver vazia, eles serão gerados de forma aleatória, caso contrário, serão definidos conforme sua ordem na lista. Outra coisa que vai ser definida é o fitness, que vai ser modificado conforme a rede é testada para saber o quão próxima ela está do modelo ideal com 100% de precisão que buscamos.

Depois da inicialização, vamos criar três métodos para a classe da rede neural, um para retornar todos os pesos da rede em uma única lista, um para incrementar o fitness da rede e outro para obter o fitness:

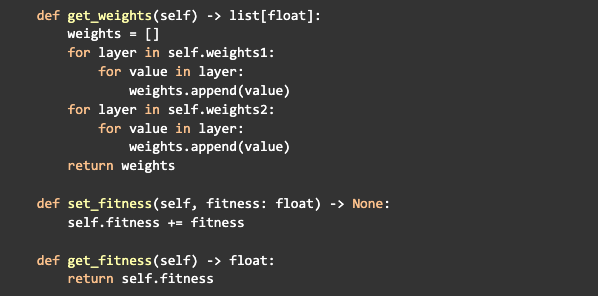
A próxima coisa a se fazer é criar um método que vai fazer a propagação da informação através da rede:

As conexões estão dispostas de modo que cada um dos inputs nos neurônios de entrada passem por um neurônio na camada oculta sozinhos e o neurônio do meio na camada oculta vai ter conexões com os dois neurônios de entrada. Dessa forma, é possível analisar a relevância de cada entrada individualmente e em conjunto no resultado final.

Ainda dentro da classe da rede neural, criaremos outro método para gerar mutações nos pesos, que será importante para adicionar mais variância aos indivíduos após o crossover. Cada peso na rede vai ter uma chance de 80% de sofrer uma mutação e essa mutação vai ter uma chance de 90% de variar 20% do valor atual e 10% de receber um valor novo aleatório, em seguida ela vai definir os novos valores dos pesos para a rede:

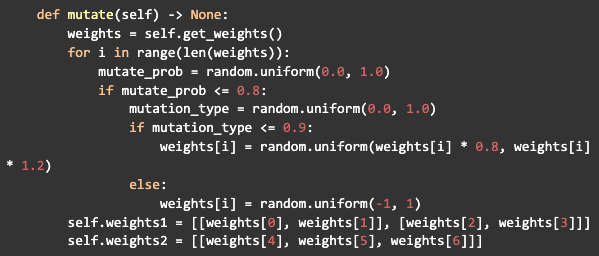
Com a rede pronta, será necessária uma função para calcular o fitness. Ela receberá como parâmetro a resposta esperada e a resposta obtida, então vai ser calculado o erro, que é a diferença absoluta entre a resposta certa e a obtida, depois vai ser retornado 1 menos o erro, dessa forma, quando o erro for 0, será retornado 1, quando ele for maior que zero, a pontuação será menor que 1:

Por fim, precisamos de uma função de crossover para gerar os novos indivíduos da população e uma função para selecionar os indivíduos:

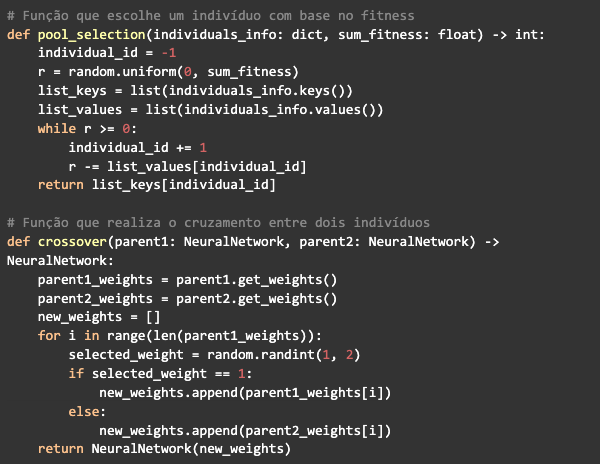
A seleção é feita utilizando um algoritmo conhecido como pool selection, ele vai receber um dicionário contendo os ids referentes à posição dos indivíduos no array da população e seu respectivo fitness, bem como a soma do fitness de todos os indivíduos. Vai gerar um número aleatório entre 0 e a soma do fitness e começar a subtrair o valor do fitness de cada indivíduo desse número gerado, quando for menor ou igual a zero, ele retorna o id do indivíduo que parou.

Assim, todos os indivíduos têm uma chance de serem escolhidos para fazer o crossover, mas a sua chance de ser escolhido vai ser proporcional ao tamanho do fitness do indivíduo.

Já a função do crossover só vai pegar os pesos de cada um dos parentes selecionados e compor os pesos do novo indivíduo, escolhendo de forma aleatória de um dos dois parentes, então ao final ela retornará o indivíduo gerado.

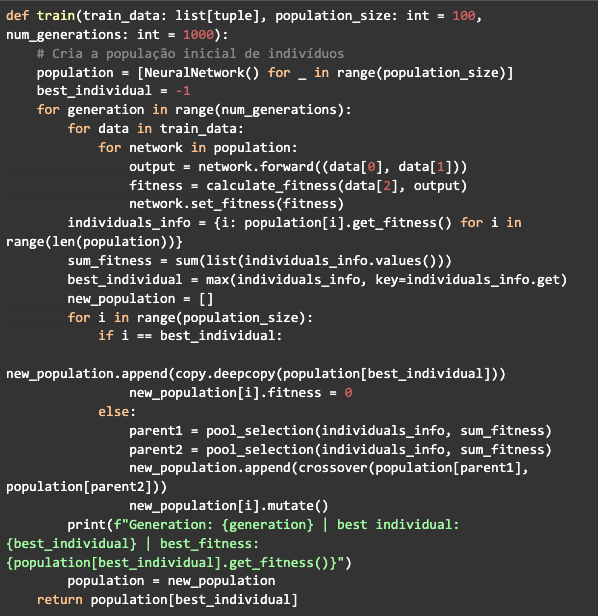
Agora basta juntar a classe da rede neural e as funções que criamos até aqui em uma nova função para treinar a rede. Essa função receberá os dados de treinamento, o tamanho da população e o número de gerações. Vai criar um array do tamanho definido para a população com objetos da classe NeuralNetwork que serão os indivíduos. Vai ter um loop referente a geração e dentro dele terão outros dois loops, o primeiro vai pegar cada valor na lista de dados, passar por cada indivíduo fazendo a propagação, calculando e definindo o fitness.

Em seguida será gerado o dicionário com os ids e o fitness de cada indivíduo, logo após será calculada a soma do fitness e definido o melhor indivíduo. Então o segundo loop vai gerar uma nova população, selecionando os indivíduos com o pool selection e fazendo o crossover, mas ao mesmo tempo preservando o melhor indivíduo encontrado na geração, de modo que ele não passe pelo crossover e não sofra mutações para não alterar sua precisão. Depois de passar por todas as gerações, a função de treinamento vai retornar a rede do melhor indivíduo:

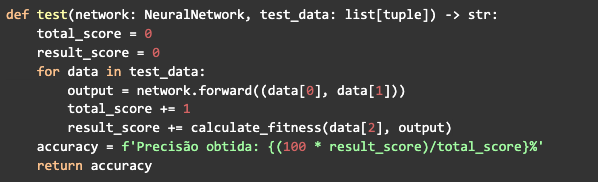
Para finalizar, basta escrever uma função para testar a rede, ela vai receber a rede do melhor indivíduo e um conjunto de dados de teste, vai fazer a propagação e calcular o fitness para todos os dados. Duas variáveis vão medir o desempenho da rede, em uma vai ser adicionado o valor máximo para o retorno do fitness para cada iteração que é 1 e em outra será adicionado o valor obtido. Então ao final a função retornará a precisão obtida, que vai ser uma simples regra de três com as variáveis que estão medindo o desempenho. O total_score vai ser 100% de precisão e o result_score é o que vai ser calculado:

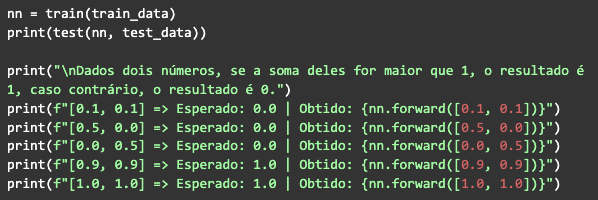
Feito isso, basta chamar a função de treinamento, depois a de teste, com os dados que geramos no início, executar e observar o resultado:

Conclusão

A Inteligência Artificial tem se mostrado uma das áreas mais promissoras da computação nos últimos anos, e o Machine Learning tem despertado um papel fundamental nessa revolução. Em particular, as redes neurais são uma das técnicas mais poderosas de Machine Learning, e o algoritmo genético é uma abordagem interessante para otimizar a performance dessas redes.

Neste artigo, mostrei como implementar uma rede neural do zero em Python, utilizando o algoritmo genético para otimização, sem utilizar bibliotecas externas. O código apresentado pode ser uma boa base para quem deseja entender como implementar redes neurais e algoritmos genéticos.

Esse exemplo que utilizamos tem uma topologia fixa e é projetado para resolver um único problema, mas ele pode ser adaptado para mudar a topologia de forma estática e resolver diferentes problemas. Porém, existem soluções mais sofisticadas que também utilizam algoritmos genéticos e que além dos pesos, também evoluem a topologia da rede dinamicamente. Um exemplo é o NEAT e você pode conferir uma forma de implementar esse algoritmo no meu repositório do GitHub.

Até logo!