Inteligência Artificial com Lógica Fuzzy e sua aplicação no mundo real

Neste tutorial vamos aprender como a Lógica Fuzzy pode nos auxiliar a expressar incertezas de modo mais consistente, por meio dos conjuntos nebulosos, “ao invés de simplesmente pertencer ou não pertencer e assim lidar com a ambiguidade da informação e a incerteza do mundo real".

Diversas ferramentas tecnológicas atuais tem nos possibilitado fornecer melhores orientações em diversas áreas na melhoraria de serviços. Dentre as técnicas de Inteligência Artificial (IA) a mais comumente utilizadas no desenvolvimento de sistemas inteligentes, destacam-se as redes neurais artificiais (RNA), as redes neurais convolucionais (RNC), o Support Vector Machine (SVM), a Lógica Fuzzy e as Árvores de Decisão (AD).

No meu artigo anterior sobre O uso de Inteligência Artificial para classificação com técnica de Árvore de Decisão, eu explico como as ADs podem gerar regras do tipo SE...ENTÃO, pelas quais podemos utilizar também em conjunto com a Lógica Fuzzy, tornando um trabalho mais abrangente e robusta no que diz respeito à técnicas de IA para predizer fatores que auxiliam as empresas na tomada de decisões.

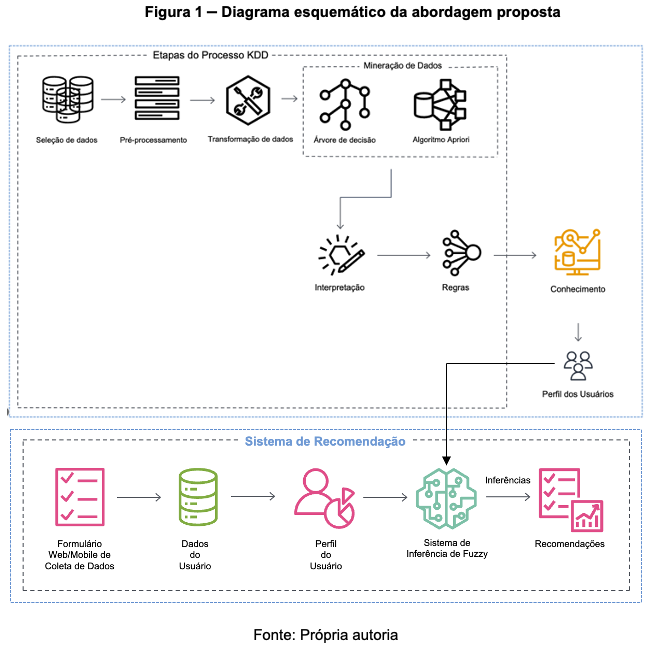
As ADs fazem parte da Mineração de Dados em conjunto com outras técnicas, como o uso do algoritmo Apriori. Na figura 1, podemos ver um conjunto de técnicas de IA que pode ser usada para o desenvolvimento de uma técnica de inteligência artificial.

Diversas ferramentas tecnológicas atuais tem nos possibilitado fornecer melhores orientações em diversas áreas na melhoraria de serviços. Dentre as técnicas de IA mais comumente utilizadas no desenvolvimento de sistemas inteligentes, destacam-se as redes neurais artificiais (RNA), as redes neurais convolucionais (RNC), o Support Vector Machine (SVM), a Lógica Fuzzy e as Árvores de Decisão (AD).

Neste artigo quero apresentar como a Lógica Fuzzy, ou Lógica Nebulosa pode nos auxiliar para desenvolver sistemas matematicamente não tradicionais. A palavra Fuzzy em inglês pode ter diversos significados, que mudam dependendo do contexto. "Nebuloso" e "difuso" são algumas das traduções mais comuns para Fuzzy (BEZERRA, 2010), mas o sentido fundamental desse adjetivo está sempre relacionado a algo vago, indistinto e incerto.

A lógica difusa ou Lógica Fuzzy é a forma de lógica multivalorada (ou multifunção), na qual os valores verdade das variáveis podem ser qualquer número real entre 0 e 1, diferentemente do que se verifica na lógica booleana, segundo a qual os valores lógicos podem ser apenas 0 ou 1. Ou seja, é um estudo que usa da lógica matemática para presumir soluções e resolução de problemas, mesmo com a imprecisão de dados e informações, mas que permite a obtenção de conclusões precisas.

Ela é considerada uma forma de lógica que lida com modelos de raciocínios imprecisos ou aproximados (ZADEH, 1973). Essa lógica permite trabalhar com problemas de decisão que não são facilmente representados em modelos matemáticos convencionais. Um controle Fuzzy procura "imitar" um agente humano por meio de uma descrição descritiva e experimental de um processo específico (ZADEH, 1973).

Dentro do campo da Inteligência Artificial, a Lógica Fuzzy é considerada um mecanismo fundamental para representar de forma apropriada o conhecimento e o raciocínio, devido à sua habilidade de trabalhar com incertezas, raciocínio aproximado, termos vagos e ambíguos, que são maneiras pelas quais as pessoas expressam seus pensamentos.

Por isso, os sistemas Fuzzy possuem a capacidade de "raciocinar" levando em conta perspectivas relacionadas à incerteza e aos processos práticos, tornando-os mais semelhantes a um comportamento "humano" (BEZERRA, 2010), conforme mostrado na Figura 2.

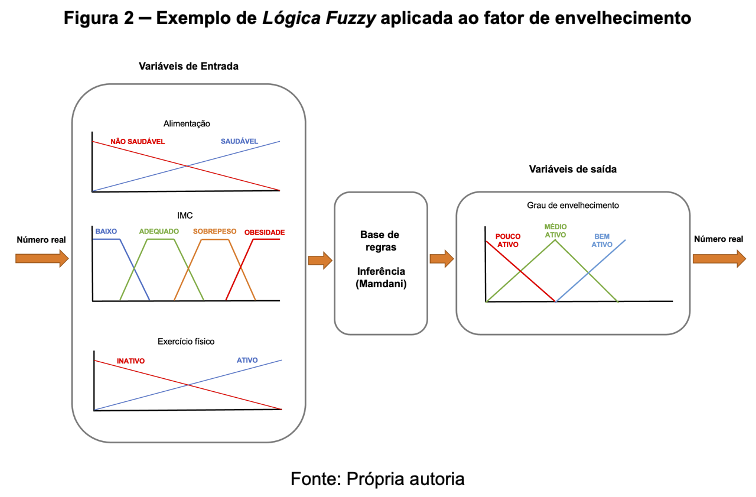
Essa técnica da área de inteligência computacional permite a representação de situações do mundo real. Além disso, foca em como codificar softwares que representem algoritmos mais próximos da forma como funciona o raciocínio humano.

Os princípios dessa lógica tiveram sua origem nos estudos do Prof. Lotfi A. Zadeh, em 1965, na Universidade da Califórnia, Berkeley. Podemos afirmar que a inteligência humana possui a qualidade de "nebulosidade", pois tem a habilidade de resumir os fatos observados e, embora possua uma ampla capacidade para adquirir informações, pode selecionar as mais relevantes. Na teoria clássica de conjuntos, podemos dizer que um elemento pertence ou não a um conjunto, ou seja, sempre temos a condição de falso ou verdadeiro (lógica bivalente).

O Professor Zadeh, como mencionado em Dubois e Gomide, propôs uma caracterização mais ampla, na medida em que sugere que alguns elementos são mais membros de um conjunto do que outros. O grau de pertinência ou grau de certeza pode, então, assumir qualquer valor entre 0 e 1, sendo que o valor 0 indica exclusão total e o valor 1 representa pertinência completa. Essa generalização aumenta o poder de expressão da função (lógica multivalente) característica (ZADEH, 1973).

A seguir é apresentada uma lista não-exaustiva de domínios de aplicação da Lógica Fuzzy.

• Sistemas especialistas;
• Sistemas multiagentes;
• Reconhecimento de padrões;
• Robótica;
• Sistemas de controle inteligentes;
• Sistemas de apoio à tomada de decisão;
• Algoritmos genéticos;
• Data Mining.

McNeil e Thro (1994) relacionam algumas características de sistemas nos quais a aplicação da Lógica Fuzzy é benéfica:

• Sistemas complexos que são difíceis ou impossíveis de modelar;
• Sistemas controlados por especialistas (humanos);
• Sistemas com entradas e saídas complexas e contínuas;
• Sistemas que se utilizam da observação humana como entradas ou como base para regras;

Sistemas que são naturalmente “vagos”, como os que envolvem ciências sociais e comportamentais, cuja descrição é extremamente complexa.

Como as relações Fuzzy funcionam em relação às funções matemáticas clássicas

No contexto matemático, a ideia de relação é expressa por meio da teoria de conjuntos. Portanto, de forma intuitiva, podemos classificar uma relação como fuzzy ao adotarmos a teoria dos conjuntos fuzzy, ou como clássica ao usarmos a teoria clássica de conjuntos para definir a relação em análise. A escolha entre esses dois modelos depende do fenômeno em estudo. No entanto, optar pela teoria de conjuntos fuzzy é geralmente mais abrangente, uma vez que engloba a teoria clássica de conjuntos.

Uma relação clássica segue a função característica da lógica clássica. Por exemplo, considere uma relação de amizade entre duas pessoas chamadas "amigos". Nesse caso, a abordagem clássica considera que nas relações humanas, ou alguém é amigo do outro ou não é, o que é uma simplificação da realidade. Já na relação de amizade fuzzy, o grau de amizade entre as pessoas é levado em conta, permitindo que dois ou mais indivíduos possam se relacionar com diferentes graus de amizade, variando de 1.0 (indicando amizade completa) a 0.0 (indicando ausência de amizade).

Formalmente, uma relação fuzzy R entre duas variáveis, x ∈ a X e y ∈ a Y, é definida por uma função que mapeia o par ordenado (x, y) no espaço X x Y para o seu grau na relação, ou seja, R: X x Y -> [0,1]. Essa definição pode ser estendida facilmente para relações de dimensões superiores.

Agora que já entendemos as definições da lógica nebulosa, vamos iniciar a declaração das variáveis de entrada e as variáveis de saída do nosso Sistema de Inferência Fuzzy. Para tanto, utilizaremos como modelo um sistema que calcula os graus de satisfação de serviços de um restaurante. As variáveis de entrada será a avaliação do serviço e a avaliação da comida. E a variável de saída será quanto de gorjeta ou taxa de serviço você estaria disposto a pagar.

Antes de começar a definir as variáveis de entrada, precisamos nos lembrar como no exemplo dos amigos acima, que estamos falando de uma abordagem não clássica, onde o grau de amizade será definido para além de é ou não é amigo, ou seja, de valores entre 1.0 e 0.0. Para isso, fazemos uso das variáveis linguísticas, as quais possuem valores que não são números. Elas são nomes de conjuntos Fuzzy, as quais podem ser representadas por meio de funções de pertinência, mostrado na figura 2 para os fatores de envelhecimento em relação ao IMC (baixo, adequado, sobrepeso, obesidade).

Usando o "problema da gorjeta" para exemplicar nossa lógica difusa

O ‘problema da gorjeta’ é comumente usado para ilustrar o poder dos princípios da lógica difusa para gerar um comportamento complexo a partir de um conjunto compacto e intuitivo de regras especializadas.

Vamos criar um sistema de controle difuso que modela como você pode optar por dar gorjeta em um restaurante. Ao dar gorjeta, você considera o serviço e a qualidade da comida, avaliada entre 0 e 10. Você usa isso para deixar uma gorjeta entre 0 e 25%.

Formularíamos esse problema como:

Iniciando a declaração das variáveis

Variáveis de entrada (inputs) - antecedentes

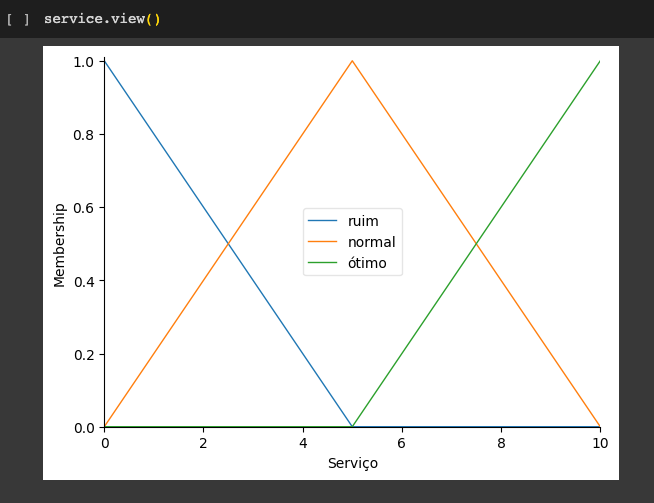
Serviço

• Universo (ou seja, faixa de valor nítido): Quão bom foi o serviço da equipe de garçons, em uma escala de 0 a 10?: ruim, normal, ótimo.
• Conjunto difuso/fuzzy (ou seja, faixa de valores difusos): ruim, normal, ótimo.

Comida

• Como você avalia a comida? (0-10): ruim, normal, ótima.
• Conjunto difuso/fuzzy: ruim, normal, ótimo.

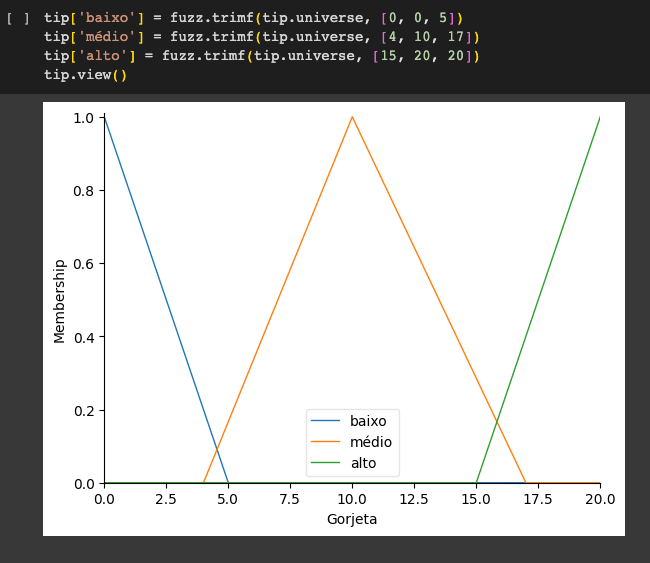
Variáveis de saída (outputs) - consequentes

Taxa de Serviço/Gorjeta

• Universo: Quanto devemos dar de gorjeta, em uma escala de 0% a 20%.
• Conjunto difuso/fuzzy: baixo, médio, alto.

Regras

• SE a qualidade da comida for ruim OU a qualidade do serviço for ruim, ENTÃO gorjeta será baixa.
• SE a qualidade do serviço for normal, ENTÃO gorjeta será média.
• SE a qualidade do serviço for ótimo E a qualidade da comida for ótima, ENTÃO gorjeta será alta.

Uso

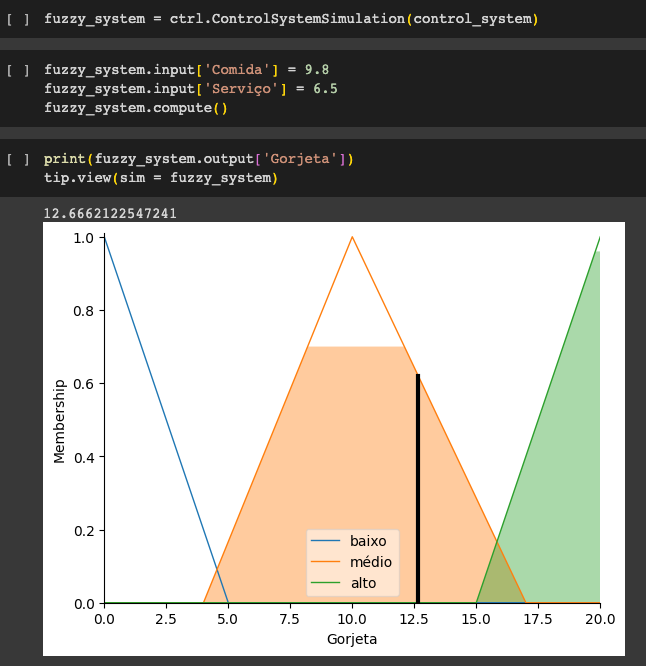
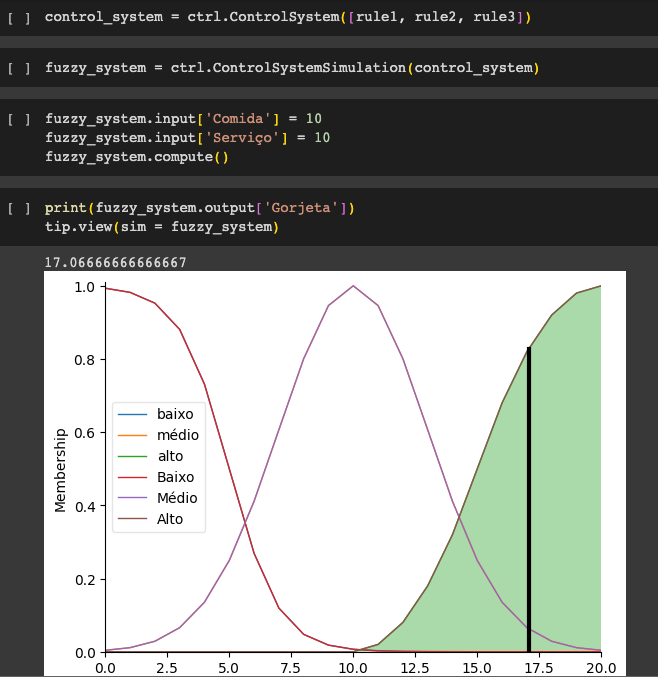
Se eu disser a este controlador que avaliei:

• o serviço como 9.8, e
• a qualidade como 6.5
• Recomendaria que eu deixasse:
• uma gorjeta de 12,6%.

Toda documentação do Scikit Fuzzy pode ser encontrada aqui.

Instalando a biblioteca scikit-fuzzy

Importando a biblioteca scikit-fuzzy

Declarando o universo/range de atuação das variáveis antecedentes e consequentes

Definindo funções de pertencimento

Imprimindo as funções de pertencimento

Imprimindo as funções de pertencimento na variável ótimo

Imprimindo as funções de pertencimento na variável ruim

Imprimindo as funções de pertencimento na variável normal

Imprimindo as funções de pertencimento para as variáveis de serviço

Imprimindo o universo de pertencimento dos valores de gorjeta

Imprimindo as funções de pertencimento da variável de gorjeta

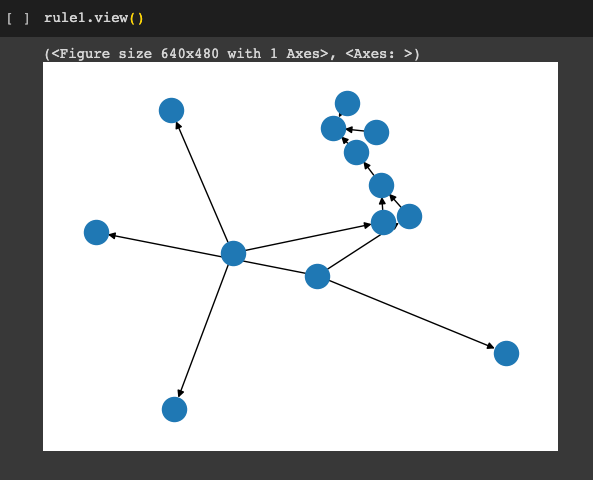
Regras difusas/fuzzy

Agora, para tornar esses triângulos úteis, definimos a relação difusa entre as variáveis de entrada e saída. Para os propósitos do nosso exemplo, considere três regras simples:

• SE a qualidade da comida for ruim OU a qualidade do serviço for ruim, ENTÃO gorjeta será baixa.
• SE a qualidade do serviço for normal, ENTÃO gorjeta será média.
• SE a qualidade do serviço for ótimo E a qualidade da comida for ótima, ENTÃO gorjeta será alta.

A maioria das pessoas concordaria com essas regras, mas as regras são confusas. Mapear as regras imprecisas em uma dica definida e acionável é um desafio. Este é o tipo de tarefa em que a Lógica Fuzzy se destaca.

Imprimindo as regra do sistema de controle fuzzy, conectando antecedente(s) a consequente(s)

Criação e Simulação de Sistema de Controle

Agora que temos nossas regras definidas, podemos simplesmente criar um sistema de controle via:

Para simular este sistema de controle, vamos criar um ControlSystemSimulation. Pense neste objeto representando nosso controlador aplicado a um conjunto específico de circunstâncias. Para dar gorjeta, isso pode ser dar gorjeta a um garçom em um bar.

Quando estivermos tentando aplicar nosso "Controle de Gorjetas" para outro estabelecimento, como por exemplo à um café, nós criaríamos outro ControlSystemSimulation porque as entradas seriam diferentes.

Imprimindo funções de pertinência usando a distribuição Gaussiana

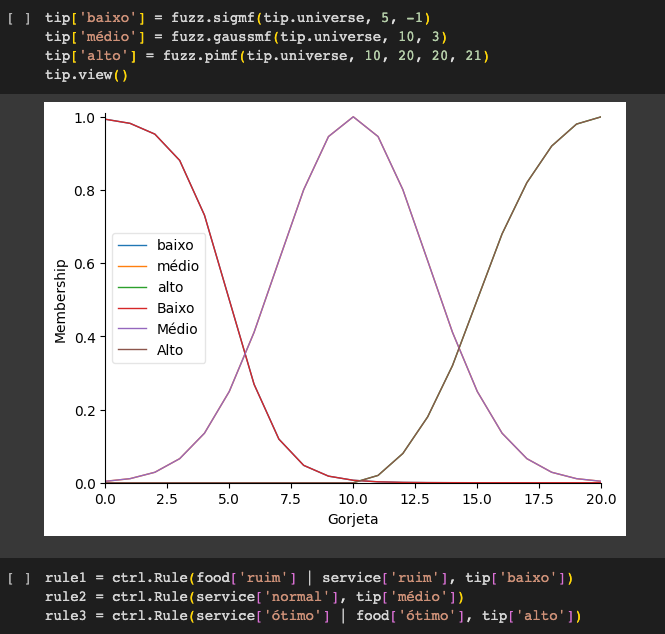
Conclusão

O poder dos sistemas difusos é permitir um comportamento intuitivo e complicado baseado em um sistema esparso de regras com sobrecarga mínima.

Observe que nossos universos de função de pertinência eram grosseiros, definidos apenas nos números inteiros, mas fuzz.interp_membership permitia que a resolução efetiva aumentasse sob demanda. Este sistema pode responder a mudanças arbitrariamente pequenas nas entradas, e a carga de processamento é mínima.

Até logo!